Originariamente Scritto da
Stefansen

Sono partito dall'idea di numero immaginario.
Possiamo scrivere un numero N come:
N=X+jY
dove X Ŕ la parte reale e Y la parte immaginaria.
Sostanzialmente, perdonate il poco formalismo, qualsiasi numero pu˛ essere rappresentato su un piano con due assi, l'uno con unitÓ 1 e l'altro con unitÓ radice(-1). Ebbene, Io mi sono domandato, e se esistesse almeno un altro asse la cui unitÓ Ŕ rappresentata dal numero s? Il numero s (numero di Stefansen) rappresenterebbe quello che Ŕ la radice(-1) per la parte immaginaria. Ecco quindi che qualunque numero N si rappresenterebbe come:
N=X+jY+sZ
dove Z Ŕ la parte "stefansenica" del numero 3D.
Un numero quindi con parte stefansenica 0 sarebbe un numero immaginario e un numero immaginario con anche la parte immaginaria 0 il classico numero naturale.
Ecco quindi che dal piano di Nyquist allo spazio di Stefansen il passo Ŕ breve.
Qui la rappresentazione 3D di un numero
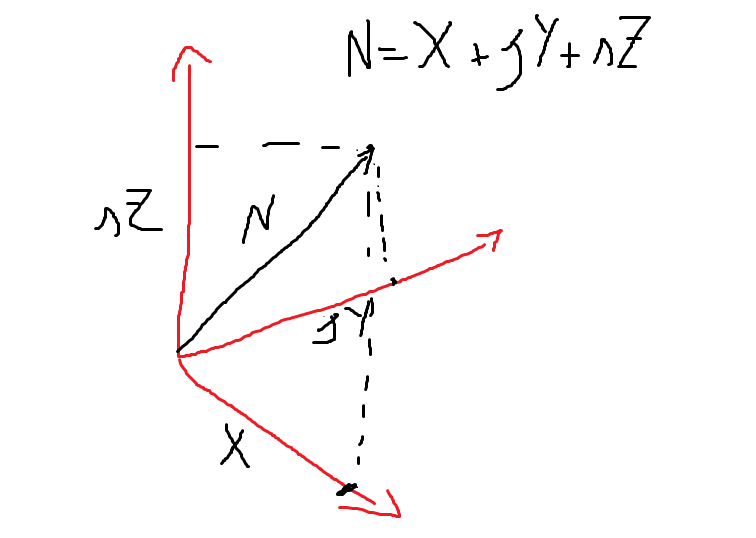
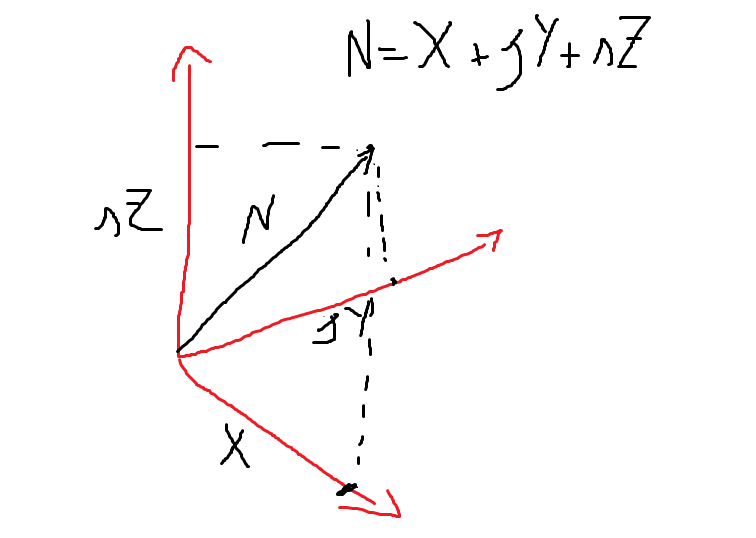




 Rispondi Citando
Rispondi Citando